
The followings is the computation of this rotation for a point: x' = x cos ? - y sin ? y' = x sin ? + y cos ? Alternatively, this rotation can also be specified by the following transformation matrix: cos θ − sin θ 0 sin θ cos θ 0 0 1 0
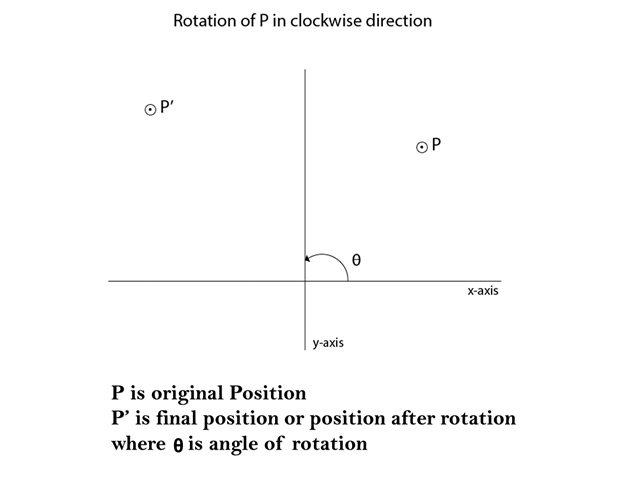

Positive and negative values for the rotation angle define counterclockwise and clockwise rotations respectively. Rotation About the Origin To rotate an object about the origin (0,0), we specify the rotation angle ?. Roughly plot the original and resultant triangles. Exercise: translate a triangle with vertices at original coordinates (10,25), (5,10), (20,10) by tx=15, ty=5. The resultant coordinates of the triangle vertices are (15,30), (15,20), and (25,20) respectively.
Basic geometric transformations are: Translation Rotation Scaling Other transformations: Reflection ShearĤ.1 Basic Transformations Translation We translate a 2D point by adding translation distances, tx and ty, to the original coordinate position (x,y): x' = x + tx, y' = y + ty Alternatively, translation can also be specified by the following transformation matrix: 1 0 t x 0 1 t y 0 0 1 Two Dimensional Transformations In many applications, changes in orientations, sizes, and shapes are accomplished with geometric transformations that alter the coordinate descriptions of objects. CS3162 Introduction to Computer Graphics Helena Wong, 2001Ĥ.


 0 kommentar(er)
0 kommentar(er)
